
이번 글에서는 p형 반도체와 n형 반도체를 서로 접촉시킨 pn junction에 대해 설명하겠습니다.
대부분의 반도체 소자는 n형 및 p형 반도체 영역 사이에 적어도 하나 이상의 junction (접합)을 포함하고 있습니다. 따라서 반도체 소자의 특성은 pn 접합의 특성과 밀접하게 연관되어 있습니다.
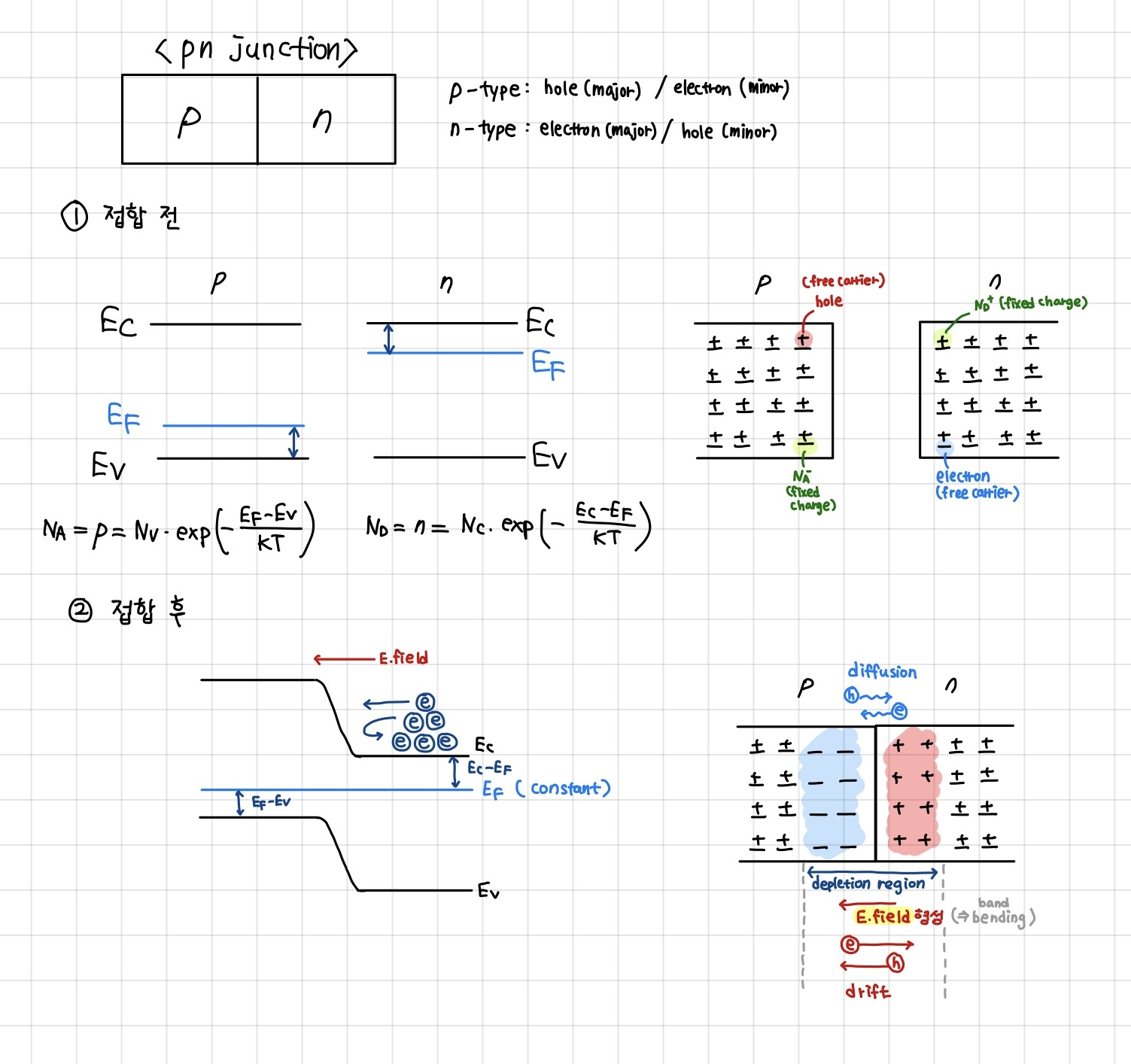
위의 그림에서 먼저 접합 전의 모습을 살펴보겠습니다. 이전의 반도체 기초 내용에 대해 설명한 것과 같이 EF는 p형 반도체에서는 EV에 가까이, n형 반도체에서는 EC에 가까이 위치해 있습니다. 그리고 EF와 EV 혹은 EF와 EC 간의 에너지 차이를 통해 캐리어의 농도를 정의할 수 있었습니다.
하지만 만약 두 반도체가 접합을 이루게 된다면, 두 번째 그림과 같은 에너지 밴드가 나타나게 됩니다. 먼저 열적 평형상태에서 EF는 constant하기 때문에 일직선으로 그려지게 되고, p 영역에서 EF-EV, n 영역에서 EC-EF를 접합 전과 같이 유지하며 에너지 밴드를 완성하면 band bending이 발생하게 되는 것을 알 수 있습니다.
이를 캐리어 관점에서 설명해보자면, 기존 p 영역에는 다수의 free carrier인 정공이, n 영역에는 자유 전자가 존재합니다. 두 영역이 접합을 이루게 되면 p영역에서 n 영역으로 정공이 확산되고, 반대 방향으로는 전자가 확산됩니다. 그렇게 되면 두 영역이 접하는 부분에서는 carrier들이 diffusion되어 사라지기 때문에 이온화된 space charge만 남게 됩니다.
p 영역에는 NA-, n 영역에는 ND+ 에 해당하는 fixed charge만 남게 되고 free carrier들은 존재하지 않게 되어 이 영역을 depletion region이라고 부릅니다. 그림에서와 같이 space charge들로 인해 depletion region에서는 E-field가 발생하게 됩니다. 이로 인해 전자와 정공이 drift에 의해 이동하게 됩니다. 이는 diffusion으로 인한 이동 방향과 반대 방향으로 형성됩니다.
평형상태에서는 diffusion에 의한 이동과 drift에 의한 이동이 균형을 이루게 되고 이에 따라 carrier의 순 이동량이 0이 되므로 depletion region은 더이상 넓어지지 않고 유지됩니다.
즉, 열적 평형상태에서는 전자와 정공에 작용하는 diffusion force와 E-field가 균형을 이루게 되어 depletion region의 width가 유지됩니다.
이를 그림으로 다시 한 번 정리하자면 아래 그림과 같습니다.
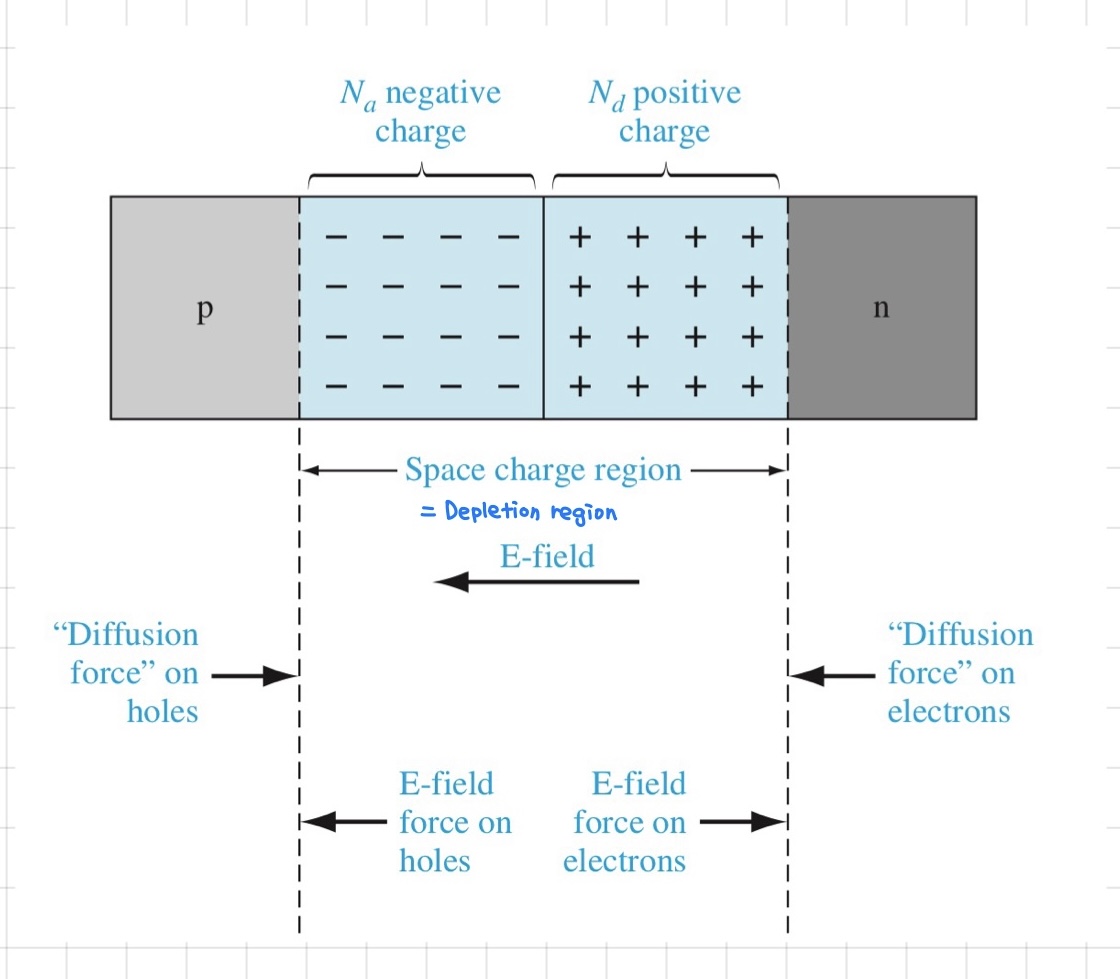
위에서 설명한 바와 같이 pn junction을 이루게 되면 외부에서 bias가 인가되지 않는 상태에서도 아래와 같이 band bending이 발생하게 됩니다.
이때, 내부적인 potential 차이가 발생하게 되는데, 이를 built-in potential, Vbi라고 합니다.

이 built-in potential을 수식을 통해 정의해보도록 하겠습니다.
Built-in potential은 그림에서도 알 수 있듯이 p와 n 영역의 EF 차이에 의해 결정됩니다. 이로부터 아래의 식을 통해 built-in potential을 정의할 수 있습니다.

위에서 설명했듯이, space charge들이 각 영역에 분리되어 있는 pn junction에서는 E.field가 발생하게 됩니다. 여기서는 charge density로부터 E.field를 정의해보도록 하겠습니다.
Uniform한 doping에 abrupt junction approximation을 가정한다면, volume charge density distribution은 아래와 같은 그림으로 나타낼 수 있습니다.
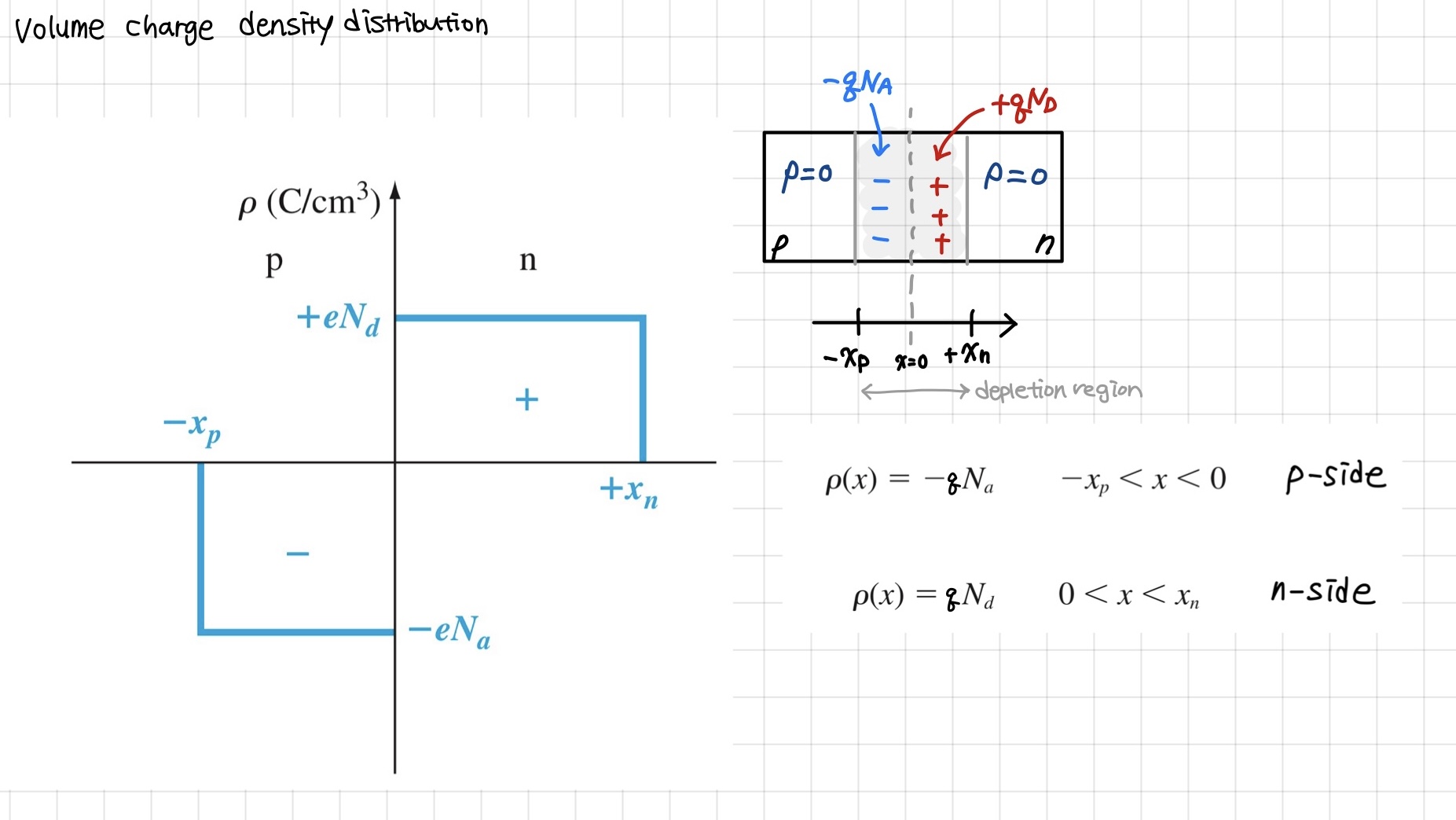
계속 설명한 바와 같이 p 영역에는 acceptor 이온이 음의 전하를 띤 채로 존재하고, n 영역에는 donor 이온이 양의 전하를 띤 채로 위치해 있습니다. 여기서 각 영역에서 접합 면을 기준으로 depletion영역의 width는 각각 xn, xp로 정의됩니다.
Poisson's equation을 이용하여 E.field에 대한 수식과 그래프를 완성하면 다음과 같습니다.

여기서 알 수 있는 중요한 것은 도핑 농도와 depletion region의 width를 곱한 값은 n 영역과 p 영역이 같은 값을 보인다는 것입니다. 이는 volume charge density distribution 그래프에서 x축을 기준으로 오른쪽과 왼쪽의 넓이가 같다는 것과 동일한 의미입니다! 만약 여기서 p 영역의 도핑 농도가 더 높은 p+n junction (one-side junction)의 경우에는 NA의 값이 증가하게 되므로 NAxp = NDxn 의 관계를 유지하기 위해서는 xp가 줄어들게 됩니다. 즉, 도핑 농도가 증가하면 depletion region의 width는 감소하게 됩니다.
다음으로는 위에서 구한 E.field 식을 통해 potential을 구해보도록 하겠습니다.
Potential을 적분하면 E.field를 구할 수 있으므로 반대로 E.field를 적분함으로써 potential을 정의할 수 있습니다.
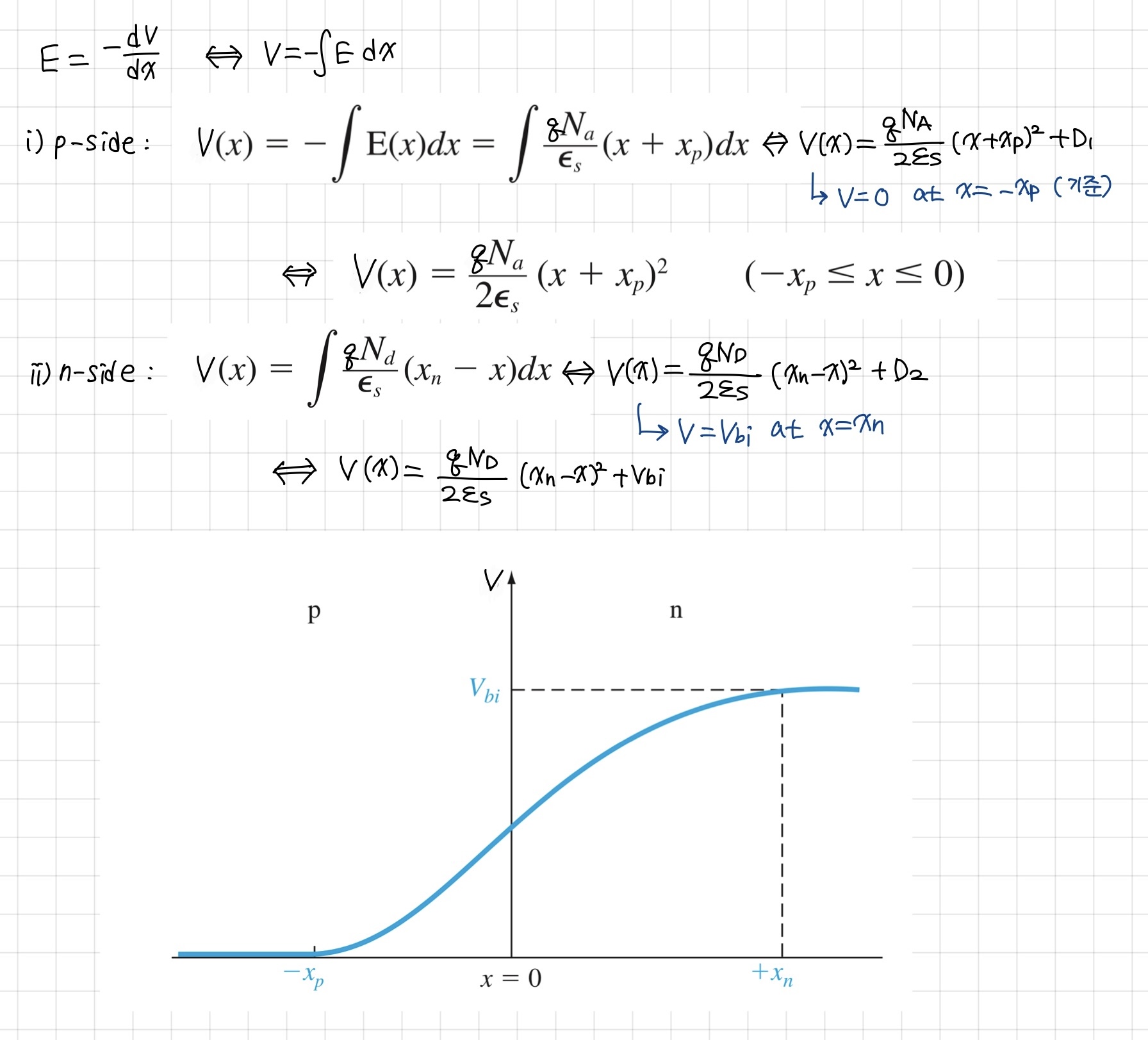
이때, potential의 기준점은 x = -xp에서 V = 0, x = xn에서 V = Vbi로 두고 계산하면 위와 같은 결과가 나오게 됩니다.
또한 x = 0에서 각 영역에 대한 potential 식은 같아야 하기 때문에 이로부터 depletion region의 width를 정의할 수 있게 됩니다.

여기서 주목할 점은 depletion region의 width는 도핑 농도에 반비례하다는 사실입니다.
이제까지는 외부에서 bias가 인가되지 않는 상태에서의 pn junction에 대해 공부해 보았습니다. 그렇다면 pn junction에 외부에서 전압이 가해진다면 어떻게 변하게 될까요?

먼저, p 영역에 - 전원, n 영역에 + 전원을 인가하는 reverse bias의 경우를 살펴보겠습니다.
E = -qV 식에 의해, p 영역의 에너지 밴드는 위로 상승하고 n 영역의 에너지 밴드는 아래로 하강하게 됩니다. 이렇게 되면 기존에 Vbi의 크기로 존재하던 potential 장벽은 더욱 높아지게 되고, 이때 외부에서 인가된 전압이 모두 이 band bending에 쓰인다고 가정한다면 그 크기는 Vbi + VR이 됩니다. 이렇게 장벽이 높아지면 diffusion에 의해 carrier들이 이동하는 것을 막게 됩니다.
외부에서 bias가 인가됐으므로 더이상 EF는 일정하게 유지되지 않고 EFn, EFp로 분리됩니다. 또한 각 영역에 존재하는 majority carrier는 전원에 의해 접합부에서 먼 곳으로 이동하게 되므로 depletion region의 width는 더욱 증가하게 됩니다.
반대로 p 영역에 + 전원, n 영역에 - 전원을 인가하는 forward bias의 경우를 살펴보겠습니다.
E = -qV 식에 의해, p 영역의 에너지 밴드는 아래로 하강하고 n 영역의 에너지 밴드는 위로 상승하게 됩니다. 이렇게 되면 기존에 Vbi의 크기로 존재하던 potential 장벽은 낮아지게 되고, 이때 외부에서 인가된 전압이 모두 이 band bending에 쓰인다고 가정한다면 그 크기는 Vbi - VF로, potential 장벽이 낮아지게 됩니다.
낮아진 potential barrier는 또한 E.field가 감소함을 나타냅니다. 감소된 E.field에 의해 carrier의 diffusion이 활발하게 발생하게 되고 이로 인해 depletion region의 width는 감소하게 됩니다.
Depletion region에서 +, - 전하들이 분리된 상태로 존재하기 때문에, pn junction에서의 capacitance를 정의할 수 있습니다.
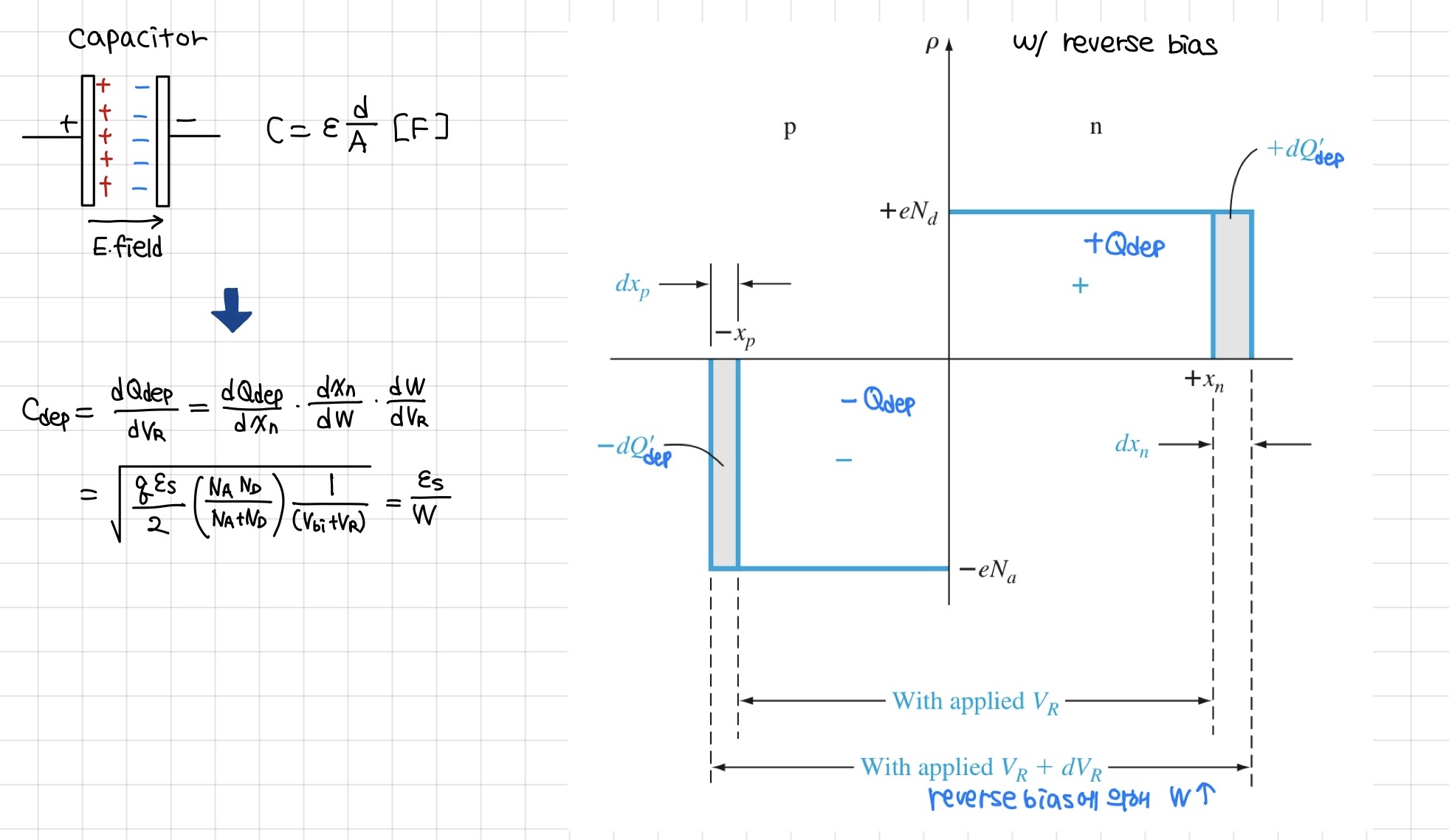
Reverse bias인 VR, VR+dVR 에서 depletion region에 존재하는 charge density를 나타내면 위와 같습니다.
증가한 dVR 만큼 추가적인 space charge 들이 발생하게 되고 이에 따라 junction capacitance를 왼쪽과 같이 정의할 수 있게 됩니다. 이 junction capacitance는 depletion capacitance라고도 불립니다. 이 capacitance 값은 결국 total depletion width에 반비례한 관계를 갖습니다. 이는 일반적인 capacitance를 정의할 때 C 값이 distance에 반비례한 것과 같은 원리로 이해하면 좋을 것 같습니다.
그러면 이 depletion cap 값을 통해 무엇을 알 수 있을까요?
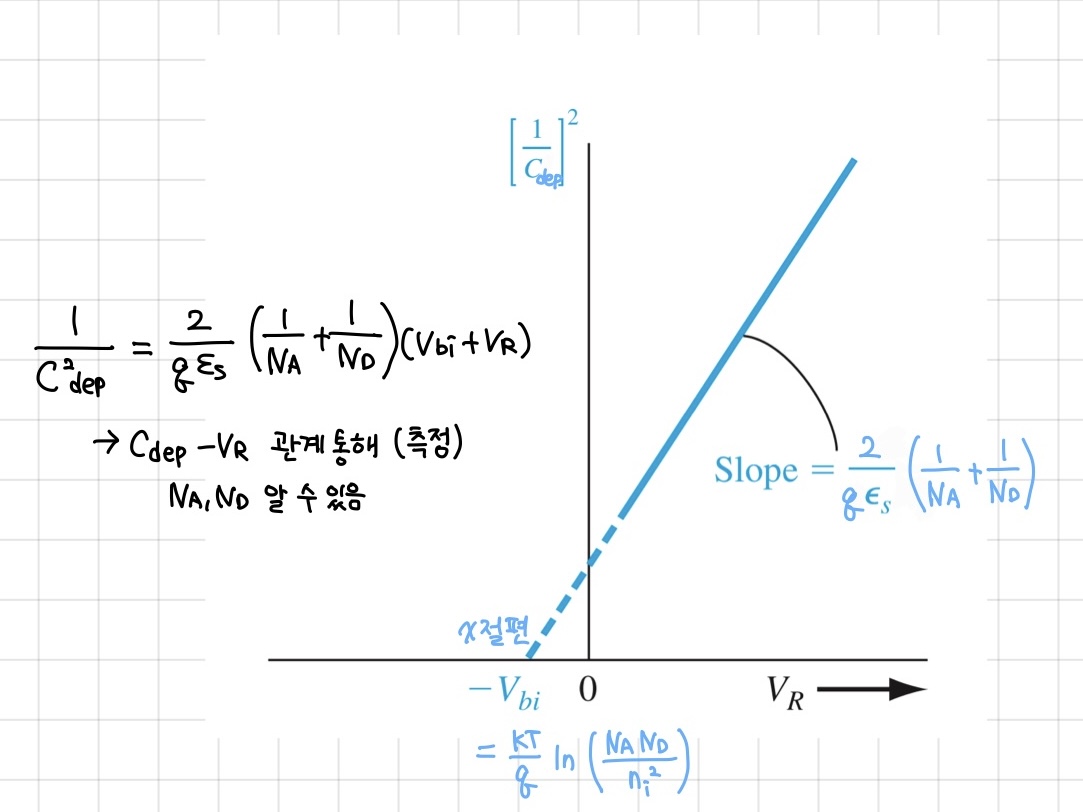
위의 그림과 같이 VR에 대한 Cdep을 측정하여 그래프를 완성하면 그래프의 기울기와 x 절편을 구할 수 있습니다. 두 값에 대한 식을 살펴보면, NA와 ND가 존재하는 것을 알 수 있습니다. 즉, VR에 따른 Cdep을 통해 pn junction의 도핑 농도를 구할 수 있습니다.
마지막으로, junction breakdown에 대해 설명하도록 하겠습니다.
앞에서 reverse bias가 인가될 때 pn junction에 미치는 영향을 살펴보았습니다. 그런데 이러한 reverse bias는 무한히 증가할 수 잇는 것이 아닙니다. 특정 reverse-bias 전압이 되면 pn junction에서 current가 급격하게 증가하는 현상이 발생하게 됩니다. 이러한 현상을 junction breakdown이라 하며 그때 인가되는 전압을 breakdown voltage라고 합니다.
이러한 junction breakdown에는 ① Zener breakdown, ② avalanche breakdown 두 가지가 존재합니다.
① Zener breakdown
Zener breakdown은 pn junction가 높은 도핑 농도로 도핑되어 있고, 높은 reverse bias가 인가될 때 발생하는 breakdown입니다.

위의 그림에서와 같이 높은 reverse bias와 고농도 도핑된 pn juntion은 매우 급격한 기울기를 가지며 bending되어 있는 형태의 energy band 를 보이게 됩니다. 이렇게 되면, p 영역의 가전자대에 존재하는 전자들이 n 영역의 전도대로 direct tunneling을 통해 이동하게 됩니다. 고농도로 도핑된 pn 접합은 위에서 확인한대로 depletion의 width가 줄어들게 되고 E = V/d에 따라 강한 E.field를 갖게 됩니다. 이러한 강한 전기장에 의해 전자가 양자 tunneling을 통해 좁아진 depletion region을 통과하여 이동하게 됩니다.
이로 인해 reverse bias가 인가될 때에도 전류가 크게 증가하는 현상이 발생합니다.
+) 이러한 Zener breakdown을 이용한 Zener diode는 reverse bias 하에서 동작하도록 설계되었는데요, 이러한 Zener diode는 주로 보호 회로로 활용됩니다. 외부에서 아주 큰 전류 (과전류)가 흘러 들어오더라도 Zener diode 양단의 전위 차는 VB (breakdown voltage)로 유지되기 때문에 회로 (IC)에 인가되는 전압을 일정하게 유지할 수 있는 역할을 합니다.
② Avalanche breakdown
Avalanche breakdown은 고농도 도핑은 아니지만, 강한 reverse bias가 인가되었을 때 발생합니다.

마찬가지로 강한 역방향 전압에 의해 에너지 밴드가 크게 휘게 되고, 이로 인해 p영역에서 n영역으로 전자가 강한 E.field에 의해 가속되어 이동합니다. 이러한 전자를 hot electron이라고 하며 이렇게 가속된 전자들은 격자 내의 원자들과 충돌하게 됩니다. 이렇게 충돌을 통해 높은 에너지를 갖는 전자들이 에너지를 전달하게 되고 이때 전달된 extra kinetic energy (△E)가 Eg보다 크다면 가전자대의 전자를 전도대로 이동시켜 가전자대의 정공과 전도대의 전자 (e-h pair)를 형성하게 됩니다. 이러한 현상을 impact ionization, 충돌 이온화라고 합니다. 이렇게 새롭게 생성된 전자와 정공 또한 높은 전기장 하에서 가속되어 또 다른 전자-정공 쌍을 계속해서 만들어 내어 전류가 기하급수적로 증폭되는 현상이 발생합니다.
위에서 설명한 두 가지 breakdown에 대한 그래프를 나타내면 다음과 같습니다.
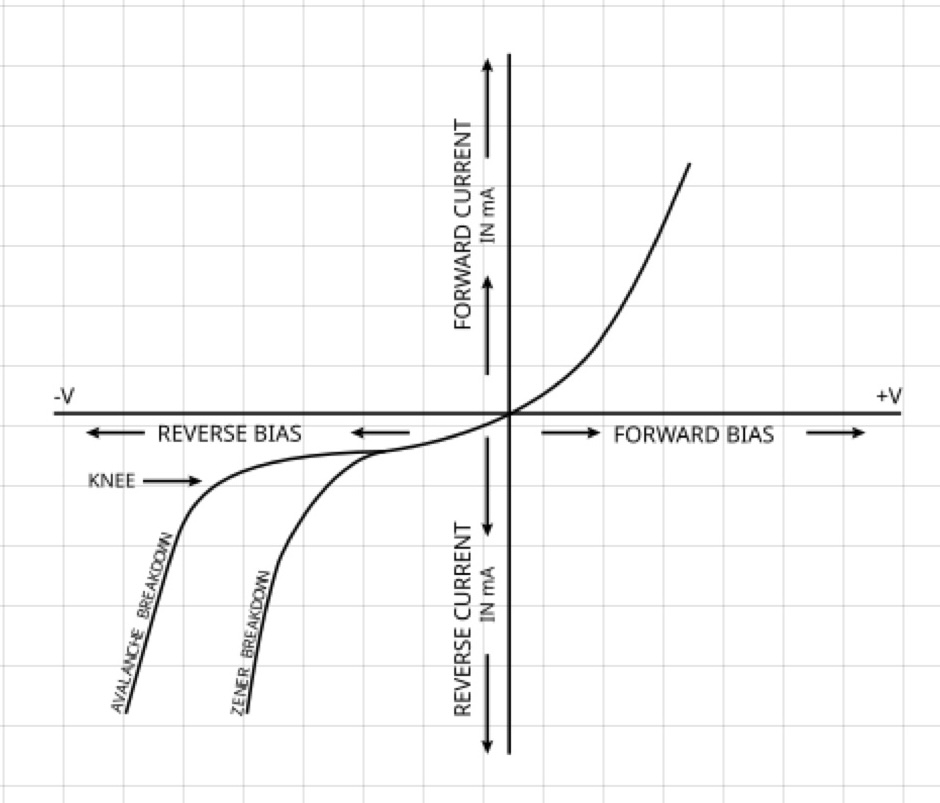
다음 글에서도 배우겠지만 reverse bias 하에서는 leakage에 해당하는 미세한 전류만 흐르지만, breakdown voltage가 되면 급격한 역방향 전류가 발생하게 됩니다.
다음 글에서는 pn junction을 기반으로 pn diode에 대해 설명해보도록 하겠습니다~
참고
NEAMAN의 반도체 물성과 소자 4th edition
Youtube| Sungho Kim: 기초 반도체 공학
'반도체 소자' 카테고리의 다른 글
| 반도체 소자(6)- MOSFET ① (1) | 2024.12.29 |
|---|---|
| 반도체 소자(5)- MOS capacitor ② (0) | 2024.12.18 |
| 반도체 소자(4)- MOS capacitor ① (1) | 2024.12.18 |
| 반도체 소자(3)- MS junction (0) | 2024.12.12 |
| 반도체 소자(2)- pn diode (2) | 2024.12.10 |



