
지금까지는 평형상태의 반도체에 대해 공부하였지만 이번 글에서는 비평형(nonequilibrium)상태의 반도체에 대해 알아보겠습니다.
앞선 반도체 기초(2) 글에서 설명했지만, 평형상태에서도 CB와 VB 사이에서 전자와 정공은 끊임없이 generation과 recombination을 반복합니다. 이때 generation은 전자와 정공이 생성되는 과정, recombination은 전자와 정공들이 소멸되는 과정입니다. 하지만 이과정들이 균형을 이루고 있기 때문에 전자와 정공의 수는 변하지 않고 유지됩니다.
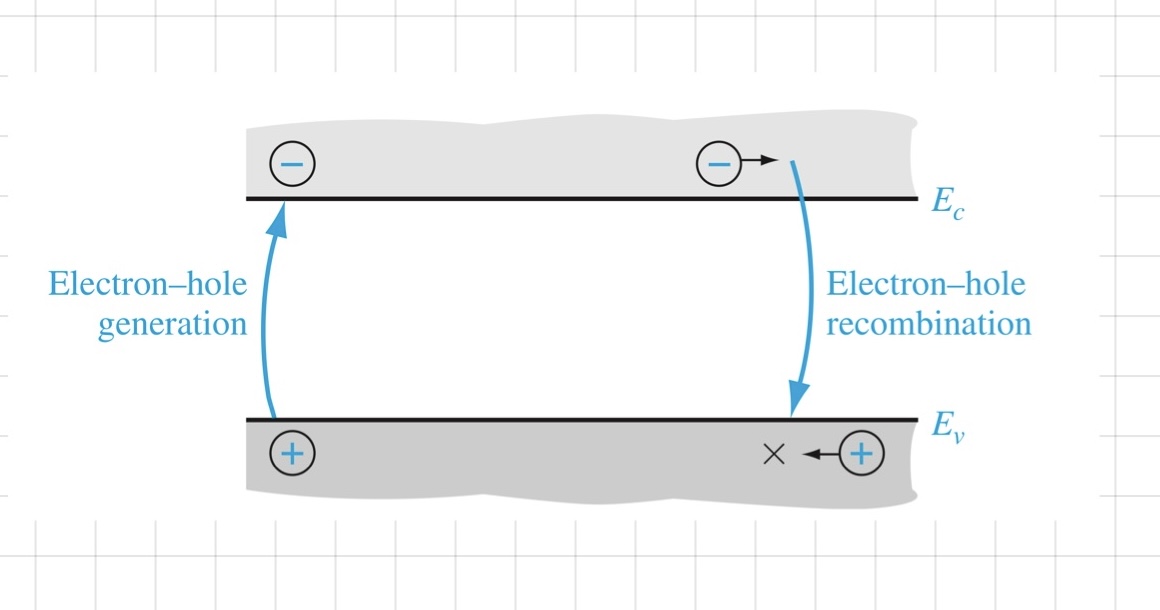
위의 그림은 direct recombination, direct generation을 나타내는 것으로, 이외에도 다양한 종류의 recombination과 generation이 존재합니다.
Recombination
① Direct recombination
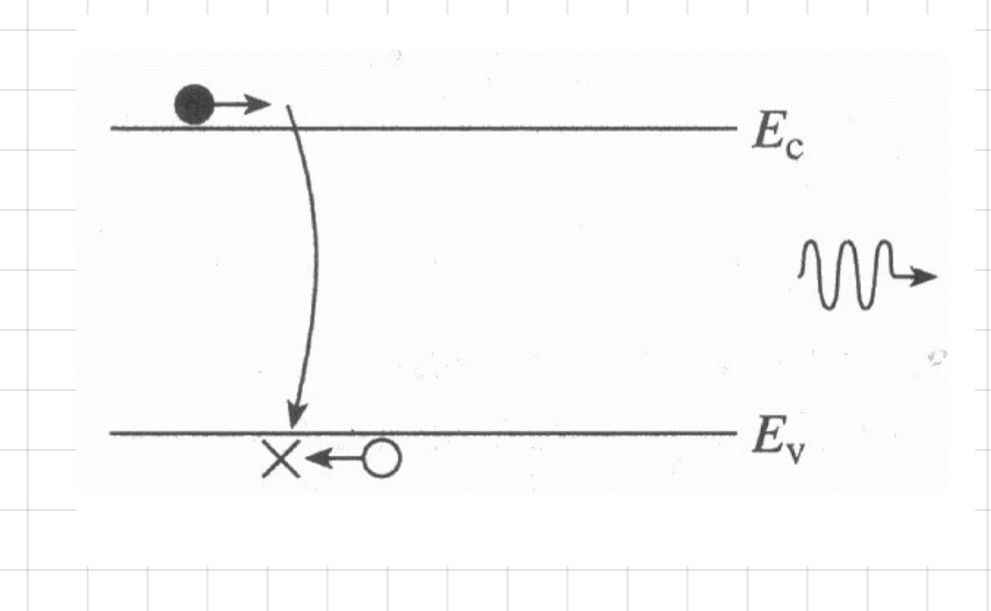
CB의 자유 전자가 에너지를 잃고 VB로 떨어지게 되어 전자와 정공이 만나 재결합하는 과정에 해당합니다. 이때 CB 에서 전자는 VB로 떨어지며 에너지를 방출하는데, 이 에너지는 빛의 형태로 방출되며 hv에 해당하는 에너지를 갖습니다.
② R-G center recombination
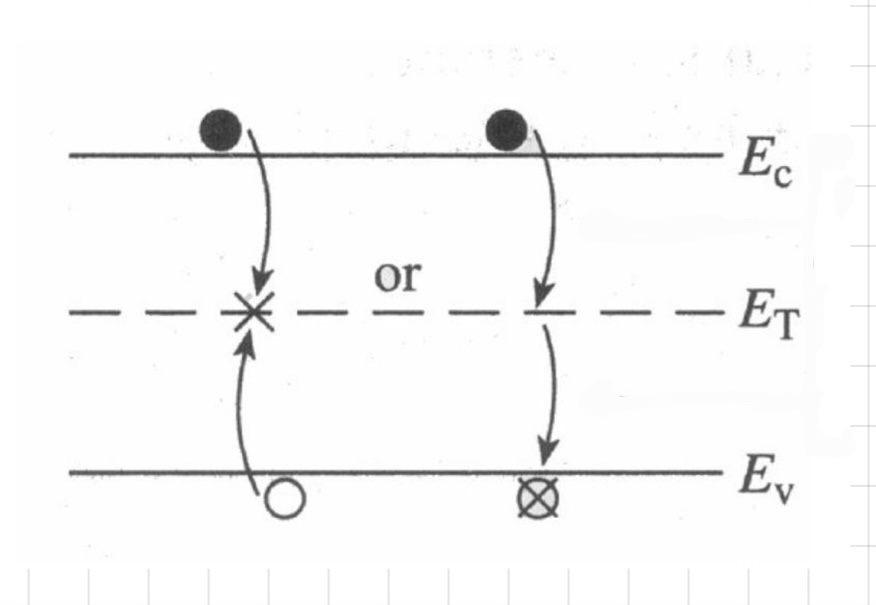
R-G center는 defect나 impurity에 의해 형성된 trap에 의해 ET에 해당하는 에너지 준위를 갖는 trapping level에 해당합니다. 이 R-G centersms band gap 중앙에 위치하게 되어 이 trap level을 통해 recombination이 발생합니다.
③ Auger recombination
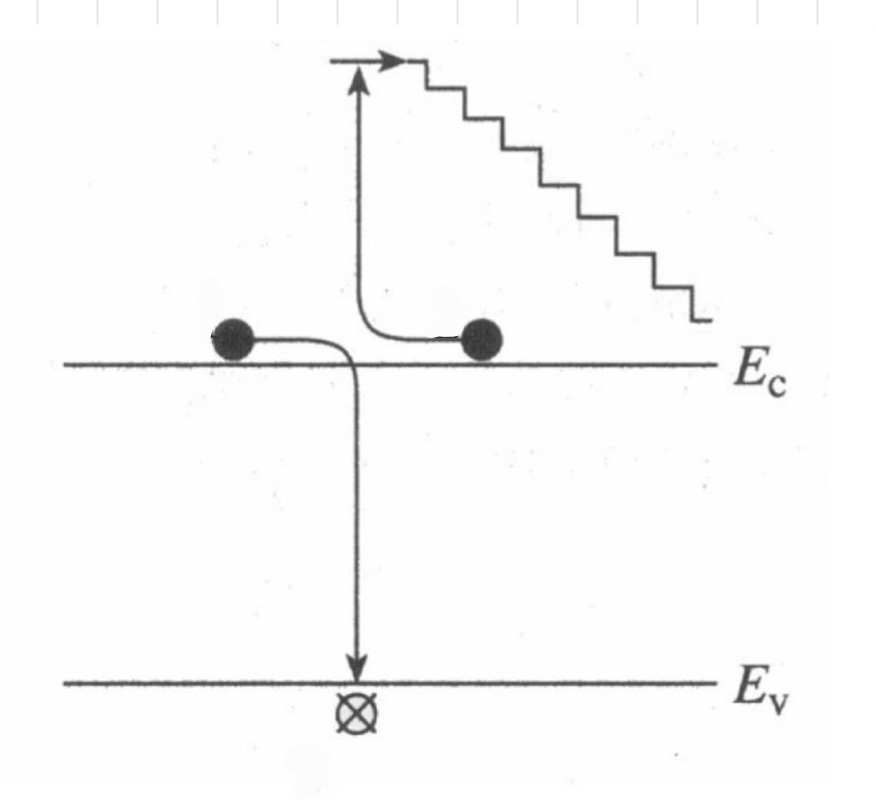
CB에 위치하는 전자가 서로 충돌할 때, 두 개의 전자 중 하나의 전자는 다른 전자에게 에너지를 전달하고 VB로 떨어지게 됩니다. 떨어진 전자는 정공과 만나 recombination이 진행됩니다. 에너지를 얻은 전자는 더욱 높은 에너지 준위로 이동하지만 lattice scattering으로 인해 에너지를 잃고 다시 EC level 근처로 떨어지게 됩니다.
Generation
① Direct generation
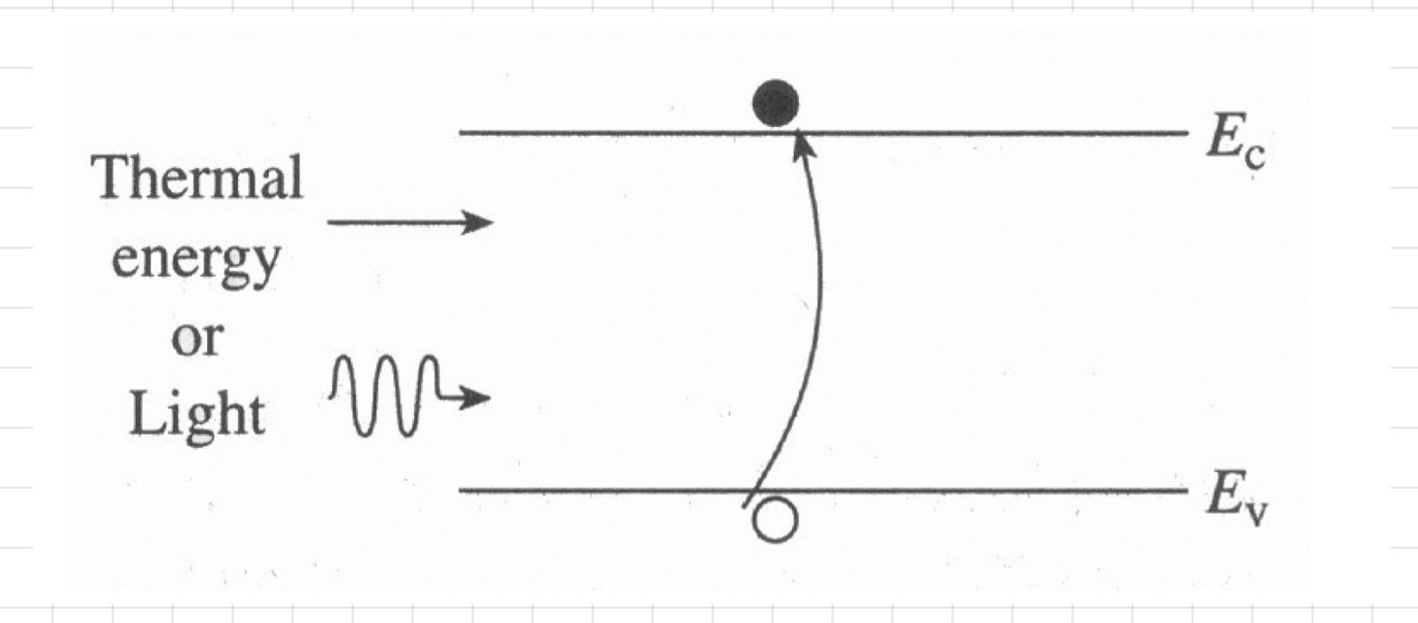
Recombination과 반대로 VB의 전자가 열이나 빛을 통해 에너지를 얻어 CB로 이동하면서 자유전자와 정공을 생성하는 과정을 의미합니다.
② R-G center generation
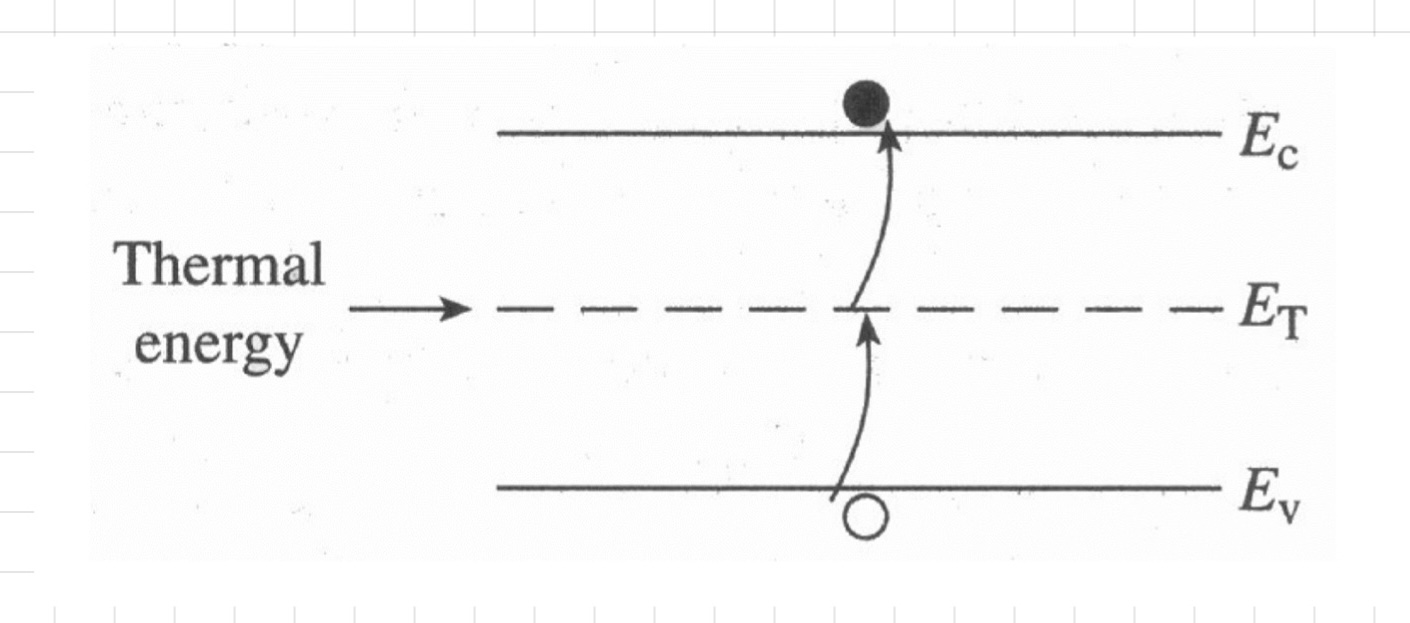
Recombination과 같이 R-G center를 통해 VB의 전자가 정공을 형성하며 trap level으로 이동하고, 이후 CB로 이동하며 자유 전자를 생성하게 되는 과정을 의미합니다.
③ Carrier generation by impact ionization
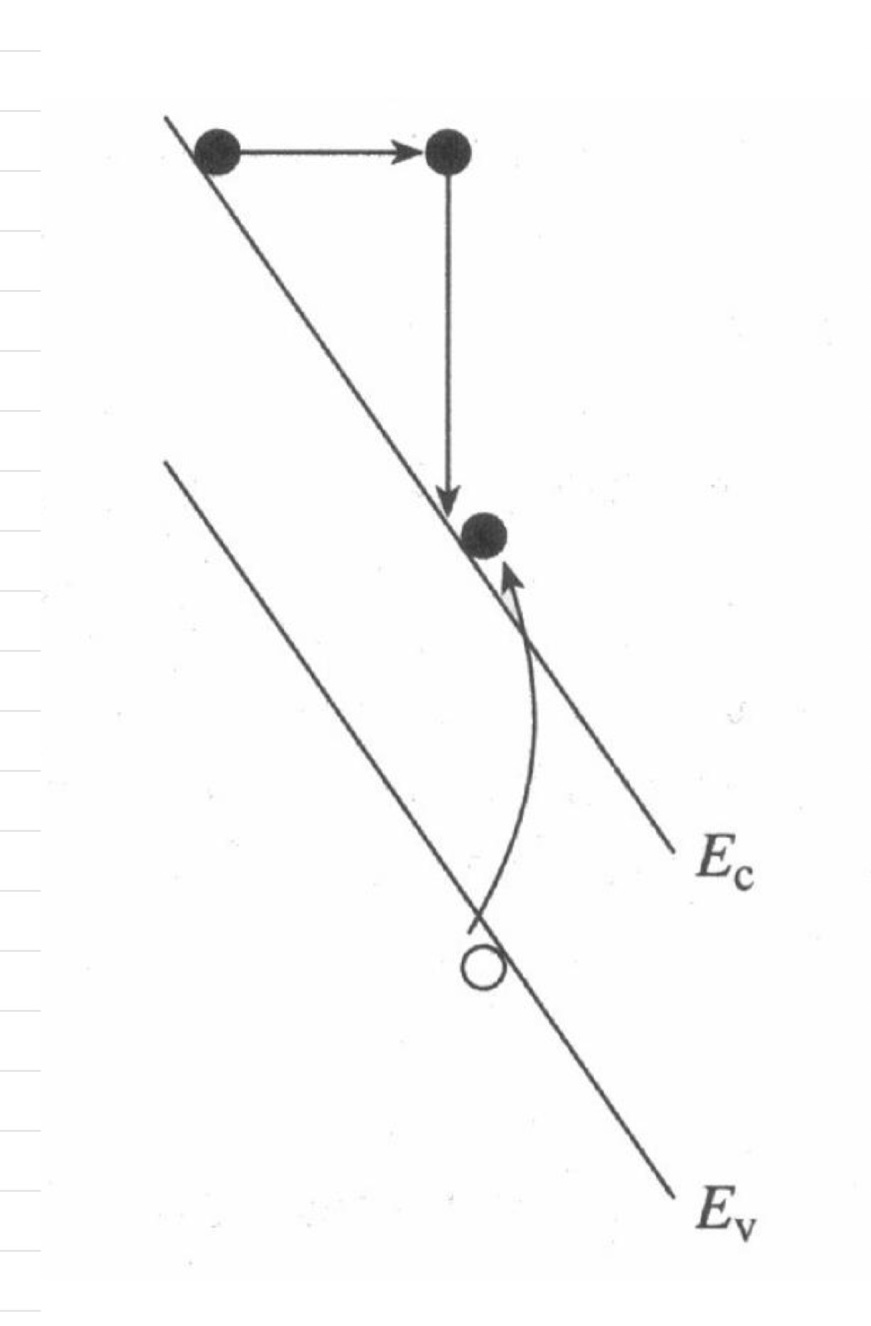
High electric field 내에서 전자나 정공이 carrier간 충돌에 의해 Eg보다 더 큰 에너지를 받게 되면 공유 결합이 깨지면서 새로운 전자-정공 쌍이 generation되는 과정에 해당합니다.
열적 평형상태의 생성률과 재결합율은 각각 G0, R0으로 나타낼 수 있으며, 단위는 [#/cm3·s]에 해당합니다.
Direct generation 의 경우, 전자와 정공은 쌍으로 생성되기 때문에
Gn0 = Gp0으로 나타낼 수 있습니다.
마찬가지로 direct recombination의 경우에도 전자와 정공은 쌍으로 재결합되기 때문에
Rn0 = Rp0으로 나타낼 수 있습니다.
또한 열평형상태에서는 이러한 generation과 recombination이 균형을 이루기 때문에 다음과 같은 식으로 정리할 수 있습니다.
Gn0 = Gp0 = Rn0 = Rp0
하지만, 외부에서 빛과 같은 자극이 주어진다면 반도체는 nonequilibrium 상태에 놓이게 됩니다. 예를 들면 고에너지의 광자들이 반도체로 입사되면, VB에 있는 전자들이 CB로 이동하며 CB와 VB에 각각 전자와 정공을 형성하게 됩니다. 즉, 전자-정공 쌍이 형성되게 됩니다. 이렇게 부가적으로 형성된 전자와 정공을 excess electrons, excess holes라고 합니다.
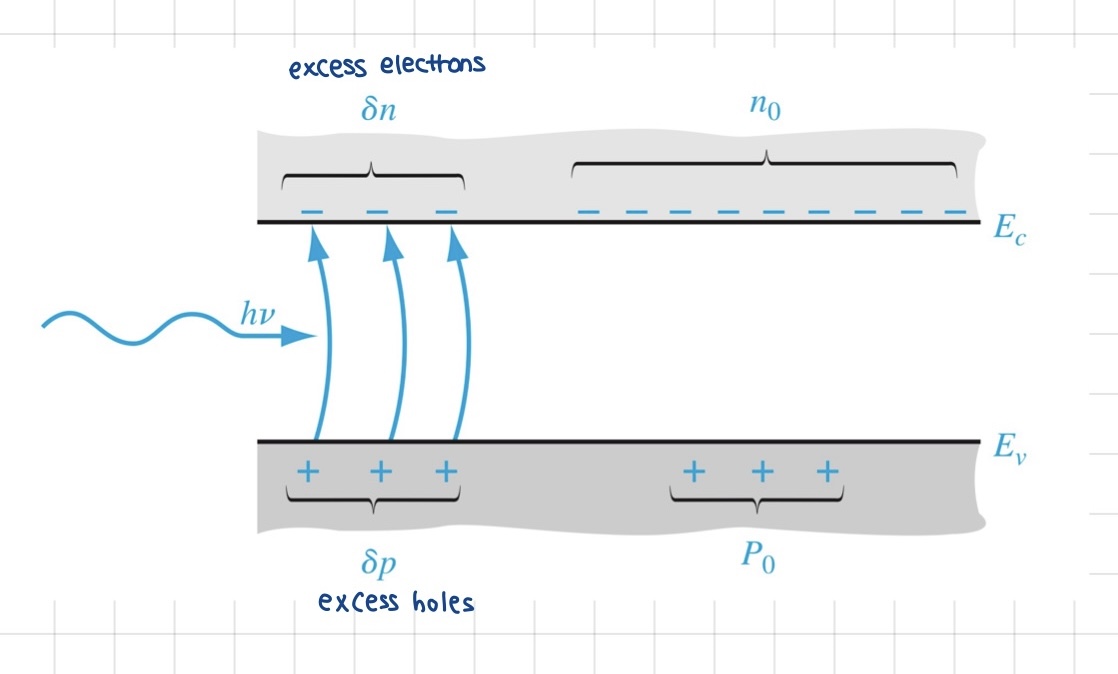
이러한 excess carrier의 생성률과 재결합률을 g', r'이라고 한다면 마찬가지로
g'n = g'p
r'n = r'p
의 식을 만족하는 것을 알 수 있습니다.
excess carrier가 생성될 때 캐리어의 농도는 평형상태일 때보다 증가하므로 다음과 같이 표현할 수 있습니다.
n = n0 + δn
p = p0 + δp
위의 식으로부터 비평형 상태에서는 np ≠ n0p0 = ni2 가 되는 것을 알 수 있습니다. 즉, mass action law가 더이상 성립하지 않게 됩니다.
이렇게 반도체 내에 excess carrier가 형성된다면 그때는 이미 thermal equilibrium 상태가 아니며 이때 페르미 에너지를 명확하게 정의할 수 없게 됩니다.
기존에는 페르미 레벨을 이용하여 열평형 상태의 전자와 정공의 농도를 아래와 같이 정의할 수 있었습니다.
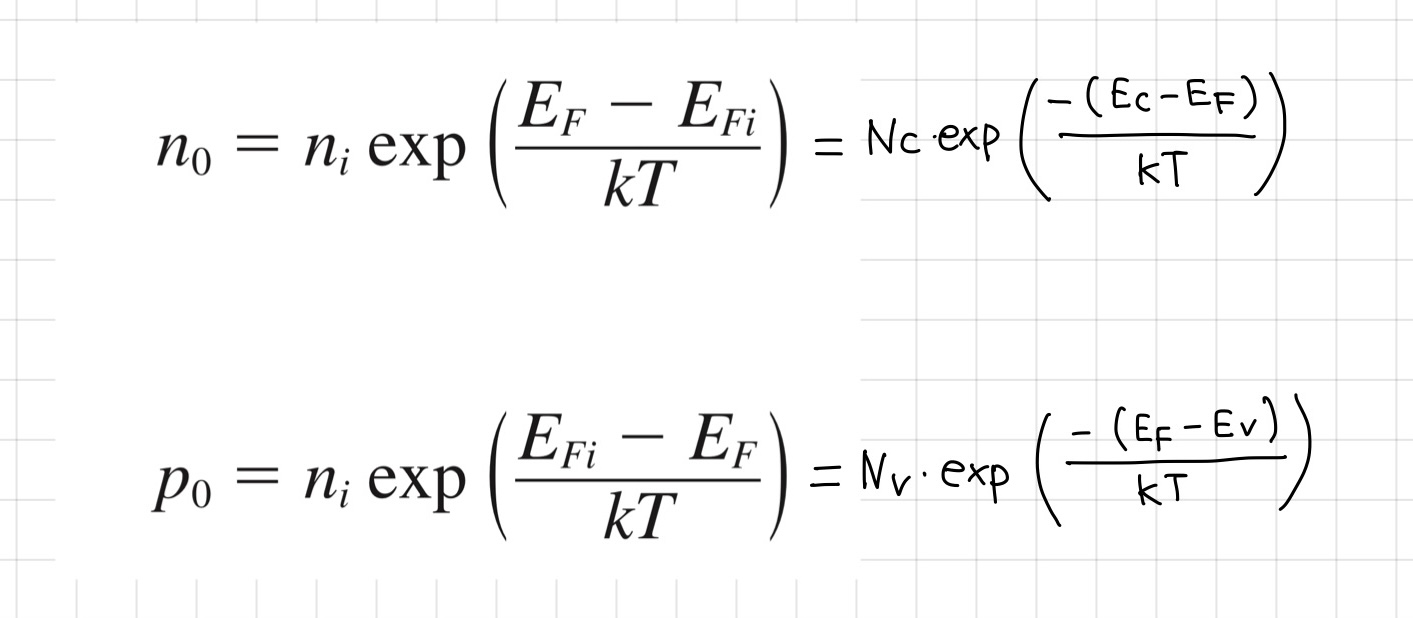
하지만 nonequilibrium상태가 되면서 위와 같은 식도 적용할 수 없게 되었습니다. 하지만 한 가지 가정을 통해 nonequilibrium 상태에서도 위와 같은 식을 정의할 수 있습니다.
<가정>excess carrier가 발생하였지만 그 양이 적어서 equilibrium에 거의 가깝게 유지되는 상황 = quasi-equilibrium 이 가정을 이용하면 아래와 같은 식을 정의할 수 있고, EFn과 EFp는 각각 전자와 정공에 대한 quasi-fermi energy level이 됩니다. 전체 전자와 정공의 농도는 quasi-fermi level의 함수로 정의할 수 있습니다.
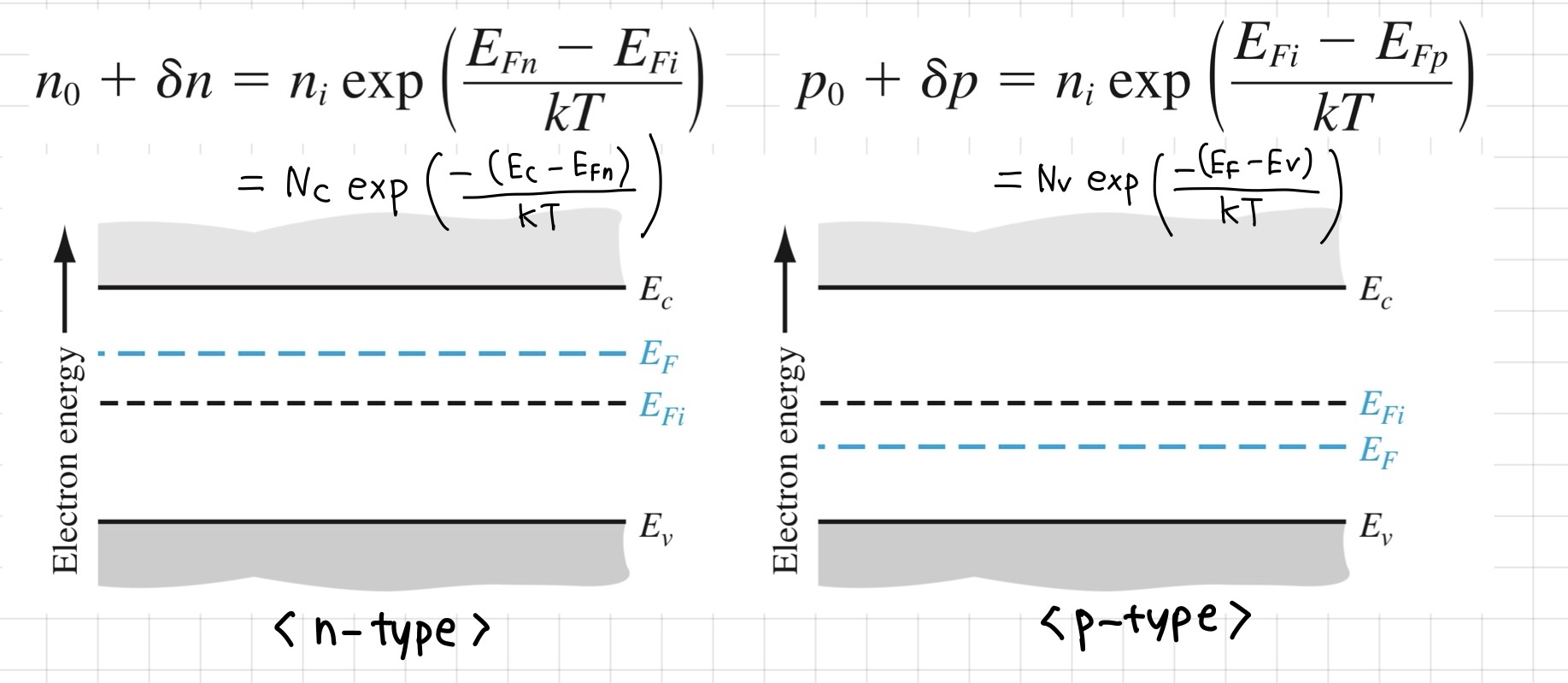
다음 글에서는 본격적으로 pn접합에 대해 설명하도록 하겠습니다~
<참고>
NEAMAN의 반도체 물성과 소자 4판
'반도체 기초' 카테고리의 다른 글
| 반도체 기초(3)- carrier transport in semiconductor (1) | 2024.11.26 |
|---|---|
| 반도체 기초(2)- silicon at thermal equilibrium (1) | 2024.11.24 |
| 반도체 기초(1)- energy bands (3) | 2024.11.20 |


